Light collection and systems throughput
This discussion is restricted to the general use of Incoherent Light Sources, such as arc lamp or quartz tungsten halogen sources. Diffraction and coherent effects are excluded. The emphasis throughout this section will be on the collection of light.
Total System Considerations
A system can include a source, collection optics, beam handling and processing optics, delivery optics and a detector. It is important to analyze the entire system before selecting pieces of it. The best collection optics for one application can be of limited value for another. Often you find that collecting the most light from the source is not the best thing to do.
F-Number and Numerical Aperture
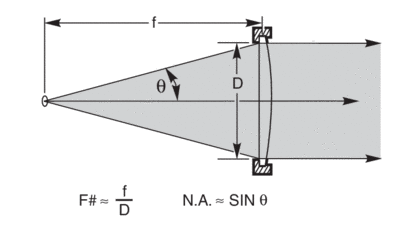
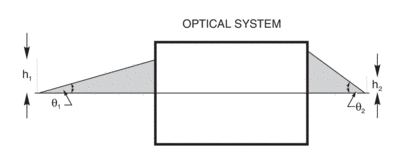
Fig.1 shows a lens of clear aperture D, collecting light from a source and collimating it. The source is one focal length, f, from the lens. Since most sources radiate at all angles, it is obvious that increasing D or decreasing f allows the lens to capture more radiation.The F-number concept puts these two together to allow a quick comparison of optics.
F-number is defined:
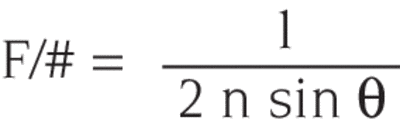
Where:
n = Refractive index of space in which the source is located
θ = Half angle of the cone of radiation as shown in Fig. 1
Though valid only for small angles (≤15°), f/D, the paraxial approximation, is widely used as F/#.
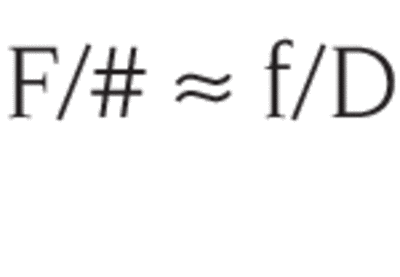
The smaller the F-number the greater the radiant flux, φc, collected by the lens.
The flux φc increases as the inverse of the square of the F/#.
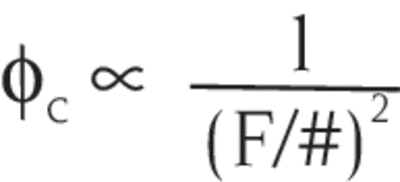
In the lexicon of photography, the F/# denotes the “speed” of the optics, with fast lenses having low F/#. The aperture control on a camera changes the F/# by using an iris diaphragm to change D.
Numerical Aperture
In microscopy and the world of fiber optics,“numerical aperture”, rather than F/#, is used to describe light gathering capability. In a medium of refractive index n, the numerical aperture is given by:
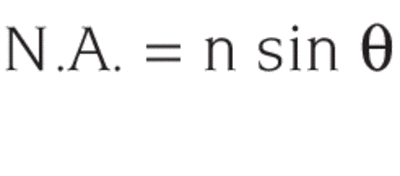
The larger the N.A., the more flux is collected. In air, the maximum N.A. is 1. Microscope objectives are available with N.A. of 0.95.
N.A. and F/# are related by:
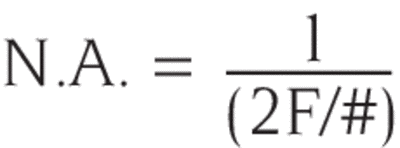
Numeric aperture is a more valuable concept for optical systems with high cone angles.
F-Number of Mirrors
Concave spherical mirrors are also used to collect and focus light. We use them for our Illuminators . The focal length of a lens can vary with wavelength due to chromatic aberration, while mirror systems are truly wideband in application. The concepts of F/# and numerical aperture also apply to mirrors. When elliptical reflectors are used, as in our PhotoMax™ Lamp Housings, F/# is used to describe the ratio of the reflector aperture to the distance between that aperture and the focus outside the ellipse.
F-Number of Non Circular Optics
We use square and rectangular mirrors in some of our products. The F-number (F/#) we quote is based on the diameter of the circle with area equal to that of the mirror. This F/# is more meaningful than that based on the diagonal, when light collection efficiency is being considered.
Collected Light and Useful Light
Since light collection varies as 1/(F/#)2, decreasing F/# is a simple way to maximize light collection. However, note, there is a difference between total radiant flux collected and useful radiant flux collected. Low F/# lenses collect more flux, but the lens aberrations determine the quality of the collimated output. These aberrations go up rapidly with decreasing F/#. Though more light is collected by a very low F/# lens, the beam produced is imperfect. Even for a point source it will include rays at various angles, far from the collimated ideal. No optical system can focus a poor quality beam to a good image of the source. So, while a low F/# singlet lens (≤F/4) may be an efficient collector, you will get such a poor output beam that you cannot refocus it efficiently. Our Aspherabs™ address this problem, and we use doublet lenses to reduce aberration in our F/1 condensers. In applications where image quality or spot size is important, a higher F/# condenser may give better results.
It is important to understand this fundamental concept, for though it is relatively easy to collect light, the quality of the beam produced and your application determine whether you can use the light collected. Our PhotoMax™ Systems are efficient collectors, but the output beams have their own limitations.
Focusing: F-Number and the Minimum Spot Size
When focusing a beam with a lens, the smaller the F-number, the smaller the focused spot from a collimated input beam, which fills the lens. (Aberrations cause some significant exceptions to this simple rule.)
Minimum Practical F-Number for Lenses
The practical limit of F/# for singlet Spherical Lenses depends on the application. For high performance imaging, the limit is about F/4. F/2 - F/1.5 is acceptable for use as a condenser with arc lamps. The lens must be properly shaped and the correct side turned towards the source (our F/1.5 plano convex condensers have much poorer aberration performance if reversed).
The number of elements must increase for adequate performance at lower F/#. F/1 camera lenses have five or six components. Our F/0.7 Aspherabs® use four. Microscope Objective Lenses approach the limit of F/0.5 with ten or more elements, and they have good performance only over very small fields.
Real Sources and Condensers
Here are some of the major considerations in selecting and using a condenser:
Transmittance
The material of any condensing lens has a limited range of spectral transmittance. Sometimes these limits are useful, for example in blocking hazardous ultraviolet (UV). Another example when working in the IR, is the use of a germanium lens with a VIS-IR source such as a QTH lamp. The lens acts as a long pass filter and absorbs the visible.
The ultraviolet transmittance of condensers and other optical elements is important when trying to conserve the limited ultraviolet components from our sources. The ultraviolet transmittance of *“quartz” or “fused silica” is very dependent on the origin of the material and on the cumulative exposure to short wavelength radiation (solarization). Our condensers are made from selected UV grade synthetic silica for the best ultraviolet transmittance.
*Quartz is the original natural crystalline material. Clear fused silica is a more precise description for synthetically generated optical material.
Thermal Problems
Although refractive index, and therefore focal length, depend on temperature, the most serious thermal problem in high power sources is lens breakage. The innermost lens of a low F/# condenser is very close to the radiating source. This lens absorbs infrared and ultraviolet. The resultant thermal stress and thermal shock on start-up, can fracture the lens. Our high power Lamp Housings with F/0.7 condensers use specially mounted elements close to the source. The elements are cooled by the Lamp Housing fan, and the element closest to the source is always made of fused silica. Even a thermal borosilicate crown element used in this position fractures quickly when collecting radiation from a 1000 or 1600 W lamp.
Collimation
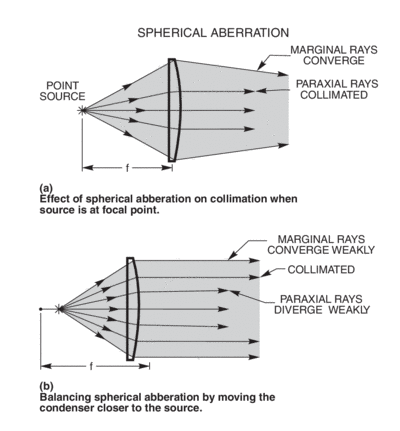
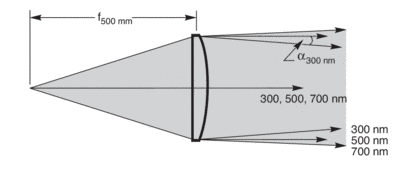
All real sources have finite extent. Fig. 2 exaggerates some of the geometry in collecting and imaging a source. Typical sources have dimensions of a few mm. Our 1 kW Quartz Tungsten Halogen Lamp has a cylindrical filament of 6 mm diameter by 16 mm long. With the filament at the focus of an ideal 50 mm focal length condenser, the “collimated beam” in this worst case includes rays with angles from 0 to ∼9° (160 mrad) to the optical axis. Most lenses have simple spherical surfaces; focusing a highly collimated beam with such a spherical optic also has limitations.
Spherical Aberration
Fig. 1 shows an ideal lens. With real single element condensers, spherical aberration causes the rays collected at high angle to converge even though the paraxial rays are collimated (Fig. 3a). You might do better by positioning the lens as shown in Fig. 3b. The best position depends on the lens, the light source, and your application. The condensers on our Research Sources have focus adjust, which allows you to find the best position empirically.
Chromatic Aberration
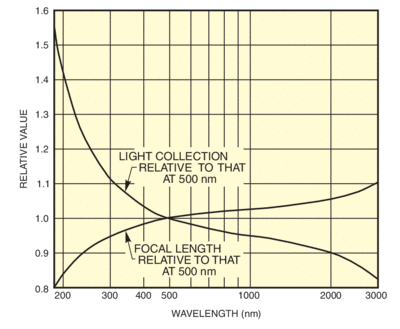
The focal length of any lens depends on the refractive index of the lens material. Refractive index is wavelength dependent. Fig. 4 shows the variation of focal length and light collection of silica lenses with wavelength. The refractive index of borosilicate crown glass and fused silica change by 1.5% and 3% respectively through the visible and near infrared, but change more rapidly in the ultraviolet. Because of this, simple lens systems cannot be used for exact imaging of the entire spectrum, nor can a simple condenser lens produce a highly collimated beam from a broad band point source (Fig. 5). Most practical applications of light sources and monochromators do not require exact wideband imaging, therefore economical uncorrected condensers are adequate. Our Research Lamp Housing Condenser Assemblies have focus adjust to position the lens for the spectral region of interest. We also provide a special version of the F/0.7 condensers for use in the deep ultraviolet.
Achromatic Lenses
Achromatic Lenses reduce the effects of chromatic aberration. Most are designed only for the visible, and include elements cemented together with optical cement. This cement will not withstand the levels of ultraviolet and infrared flux from our high intensity arc sources. The material darkens and absorbs light. If you need the imaging performance of these lenses, you should collect the light from the source using a standard condenser. Then remove the ultraviolet and infrared, and use a secondary focusing lens and pinhole to create a bright, well defined image for use as a secondary source. This secondary source may then be imaged by the achromat. Camera lenses and other achromats are valuable with low intensity or distant visible sources.
Directionality in Source Radiance
Real sources also do not radiate equally in all directions. By design, our Quartz Tungsten Halogen Lamps have the strongest irradiance, normal to the plane of the filament. We designed our lamp housings so that the optical axes of the condensers lie in the direction of highest radiance. Our 6333 100 W Quartz Tungsten Halogen Lamp emits about 3600 lumens. If this was uniformly radiated into all space, then our F/1.5 condenser would collect only 94 lumens (2.6%). In fact, the lens collects about 140 lumens.
Mirrors, An Alternative Method
Curved mirrors suffer from many of the same problems that plague lens systems such as thermal considerations, limited field of view, and spherical aberration. Nevertheless, there are advantages that make reflective optics useful in place of lenses for some collection, focusing, and imaging applications. For this reason, we use mirrors in our 7340/1 Monochromator Illuminators, Fiber-optic Illuminators, and in Oriel PhotoMax Lamp Housing
Mirrors Do Not Have Chromatic Aberration
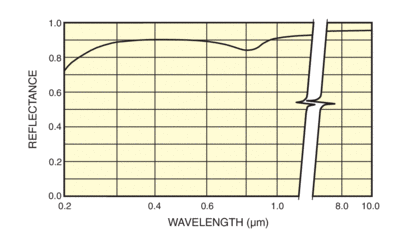
Because reflection occurs at the surface of these optics, the wavelength dependent index of refraction does not come into play. Therefore, there is no variation in how a mirror treats different incident wavelengths. Some care must be taken in choosing the mirror's reflective coating, as each coating exhibits slightly varying spectral reflectance (see Fig. 6). However, mirrors eliminate the need for refocusing during broadband source collection or imaging. Simple spherical reflectors such as front surface concave mirrors are suitable as condensers in many applications.
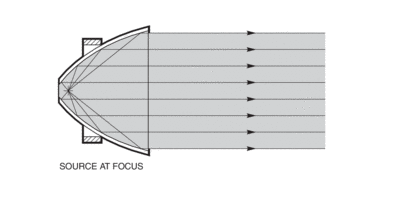
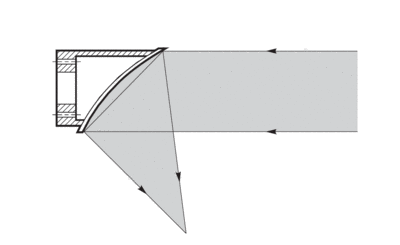
Paraboloidal Reflectors
These reflectors collect radiation from a source at the focal point, and reflect it as a collimated beam parallel to the axis (Fig. 7). Incoming collimated beams are tightly focused at the focal point. Our Off-Axis Paraboloidal Reflectorsare a circular segment from one side of a full paraboloid. The focal point is off the mechanical axis, giving full access to the reflector focus area (Fig. 8). There are no shadowing problems if you place a detector or source at the focus. Note that these mirrors do introduce significant aberrations for extended sources.
Ellipsoidal Reflectors
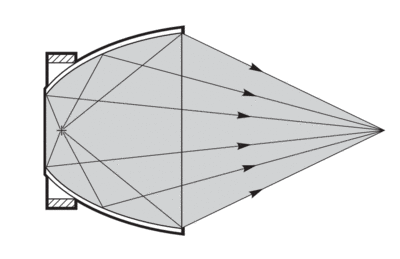
Ellipsodial Reflectors have two conjugate foci. Light from one focus passes through the other after reflection (Fig. 9). Deep ellipsoids of revolution surrounding a source collect a much higher fraction of total emitted light than a spherical mirror or conventional lens system. The effective collection F/#’s are very small, and the geometry is well suited to the spatial distribution of the output from an arc lamp. Two ellipsoids can almost fully enclose a light source and target to provide nearly total energy transfer.
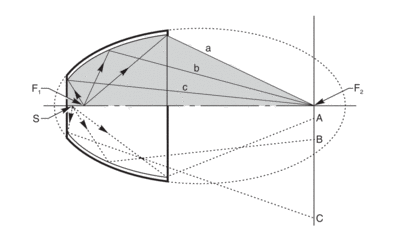
More significant perhaps is the ellipsoid’s effect upon imaging of extended sources. For a pure point source exactly at one focus of the ellipse, almost all of the energy is transferred to the other focus. Unfortunately, every real light source, such as a lamp arc, has some finite extent; points of the source that are not exactly at the focus of the ellipse will be magnified and defocused at the image. Fig. 10 illustrates how light from point S, off the focus F1, does not reimage near F2, but is instead spread along the axis. Because of this effect ellipsoids are most useful when coupled with a small source and a system that requires a lot of light without concern for particularly good imaging.
Some Limitations of the F-Number Concept
Beam Quality
The beam quality concept mentioned earlier is one of the dangers of using F/# as the only quality measure of a condenser or other optical system.
Definition Depends on Application
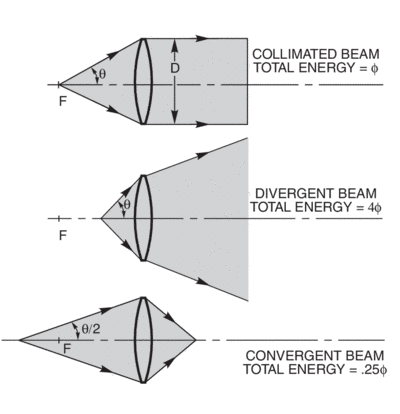
Fig. 11 shows the same lens at three different distances from a source. According to the definition of Fig.1, the F/# of the lens is f/D, but obviously the light collected by the same lens differs significantly for each position. The description should include the F/# for collection and the F/# for imaging.
A single F/# is sometimes defined for the particular optical configuration. We use f/D to compare collimating condensers. For condensers not at a focus, or other imaging systems, we use the higher of the ratios of image distance to optic diameter and source (object distance) to optic diameter. This incorrect use of F/# is somewhat legitimized as it states the worst case parameters for a system.
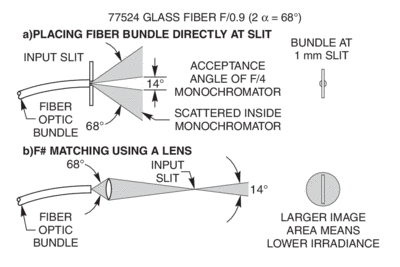
Throughput Optimization Requires More Than F-Number
Matching F/# is important through an optical system. For example, in a system using a fiber optic input to a monochromator (Fig. 12a and 12b), the output of the fiber optic, characterized by a numerical aperture or F/# value, should be properly matched to the input of the monochromator. Consideration of F/# alone does not however give a simple way of optimizing such a system. This is because F/# contains no information on source, image, or detector area. In the example, matching of F/# alone does not take into account the consequential change in irradiance of the monochromator input slit. If the F/# of the beam from the fiber is increased to match the acceptance F/# of the monochromator, the beam size on the slit increases and less light enters the monochromator. The concept of “optical extent” gives a better sense of what is attainable and what is not.
Geometrical Extent, Optical Extent, and Linear Invariant
Very often the goal in optical system design is to maximize the amount of radiant power transferred from a source to a detector. Fig. 13 shows a source, an optical system, and an image. The optical system is aberration free and has no internal apertures, which limit the beam. The refractive index is 1. Using paraxial optical theory, we can prove that:
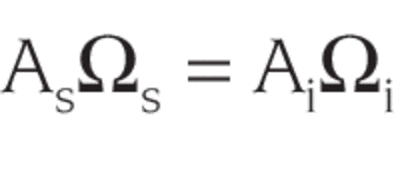
Where:
As = Source area
Ai = Image area
Ωs = Solid angle subtended at the source by the entrance aperture of the optical system
Ωi = Solid angle subtended at the image by the exit aperture.
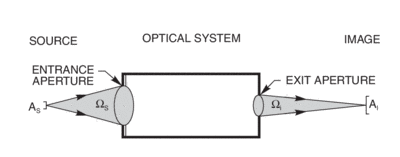
The quantity G = AΩ is the same for the source and the image, and for any other image plane in the system. G is called the geometrical extent.
If the surfaces are in media of different refractive indices, then n2G, the optical extent, replaces G. If the source has uniform (or average) radiance L, then the radiant flux, which reaches the image (often at a detector), is:
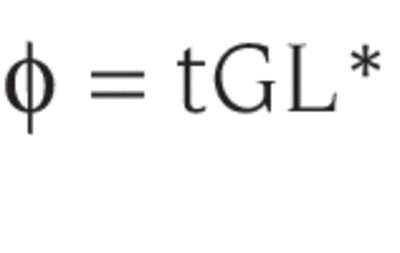
Where:
t = transmittance (t will include reflection losses and component transmittances)
*Again, an aberration free optical system is assumed. When aberrations are present, tGL becomes an upper limit on achievable flux: φ ≤tGL.
The concept of optical extent has been widely applied, though under a variety of names. These include etendue, luminosity, light-gathering power and throughput. The one dimensional version of the optical extent is applicable to rotationally symmetrical systems and is easier to work with. Fig. 14 defines h1, h2, θ1, and θ2.
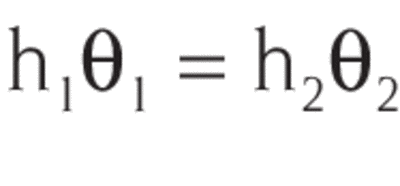
For equal refractive index, the product θ1h1 is invariant through an optical system. The product has several names including the optical invariant, Lagrange invariant, and Smith-Helmoltz invariant. When sin θ is substituted for θ, the equation is called the “Abbe sine condition”.
Any system has two values of the one dimensional invariant, one for each of two orthogonal planes containing the optical axis.Obviously, for an instrument with slits it is simplest to use planes defined by the width and height of the slit. In this case, it is important to remember that the two values of optical extent for the orthogonal planes are usually different, as input and output slits are usually long and narrow. This complicates the selection of a coupling lens for optimizing the throughput.
Importance of Optical Extent
In introducing the concept of G, we required that the optical system in Fig.13 had no internal limiting apertures.This meant that G was determined by the source area and input acceptance angle of the optical system. In this case, for more total flux through the system from a source of fixed size and radiance, all that is needed is to increase G. This is equivalent to decreasing condenser F/# as previously discussed.
Every real optical system has something in it that limits G. It could be space or economic constraints. Frequently, Glim is determined by a spectrometer. In some systems, a small detector area1 and the practical constraint on the maximum solid angle of the beam accepted by the detector limit G. When a system uses fiber optics, the aperture and acceptance angle of the fiber optic may determine Glim.
1 Complete system modeling requires attention to detector noise. Often this is related to detector area.
Whatever limits G, fixes the maximum throughput, and no amount of clever optical design can improve on that limit.
The radiant flux through the system becomes:
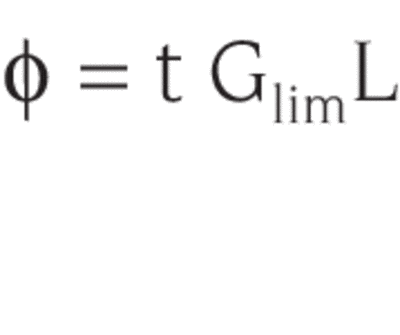
or at a specific wavelength λ:
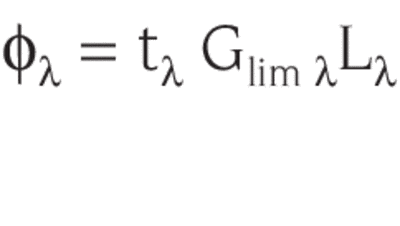
(Frequently, G can be considered independent of wavelength.)
How to Maximize the Light Through the System
First look through the proposed system, beyond the light source and condensers, for the component that limits G and, if possible, replace it with a component with a higher G. When you have finally fixed the limiting G, you can then sensibly select other components to minimize cost. (Optics cost usually increase with aperture.)
Light Source and Condenser
Select the source and collection optics to:
1. Match Glim
The collection optics should have a value of G that is as large as Glim. At smaller values, the collection of light from the source limits the total flux transfer. You can use a higher value of G. More radiation is collected, but this cannot pass through the optical system. If Glim is due to a spectrometer, the excess radiation will be lost at the slit or scattered inside the spectrometer, leading to possible stray light problems.
2. Maximize GlimL
Glim determines the product of source area and collection angle. These can be traded off within the limitation of source availability and maximum collection angle (1.17 sr for F/0.7 Aspherab®, 0.66 sr for F/1). For a given source area, you get more radiation through the system with a higher radiance (L) source. (See Table 1) (For spectroscopy, use the spectral radiance at the wavelength you need.)
Note: Aberrations introduced by the optical elements will lead to lower flux through image deterioration. Use of aberration corrected optics like Aspherabs® lead to significantly higher Glim.
Table 1 Average Spectral Radiance of Various Sources
| Source Type | Model | Input Power | Nominal Source Dimensions (mm) | Average Spectral Radiance* (W cm-2 sr-1 nm-1) |
|||
|---|---|---|---|---|---|---|---|
| 300 nm | 400 nm | 500 nm | 633 nm | ||||
| Quartz Tungsten Halogen | 6333 | 100 W | 4.2 x 2.3 | 0.0015 | 0.013 | 0.034 | 0.065 |
| Xenon Arc | 6253 | Xenon | 0.5 x 2.2 | 0.085 | 0.16 | 0.21 | 0.24 |
| 3400 K Blackbody | 0.0037 | 0.03 | 0.08 | 0.15 | |||
| Sun** | 1.4 x 1012 | 0.75 | 2.1 | 2.9 | 2.2 | ||
| HeNe Laser | 2 mW*** | 0.63 diammeter | 0 | 0 | 0 | 108**** | |
*Over the nominal area. Small regions may have a higher radiance.
**Based on extraterrestrial solar radiation.
***This is output power. Conventionally, lamps are rated by input power, lasers by output power.
****Based on a 4 x 10-3 nm line width.
Examples of Use of Invariants
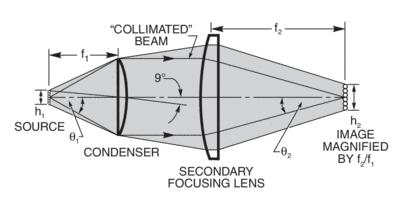
Source Magnification
Since θh is invariant, we can easily relate source and image size. Fig.15 shows this for a simple condenser/ focusing lens arrangement, and Fig. 14 for any optical system.
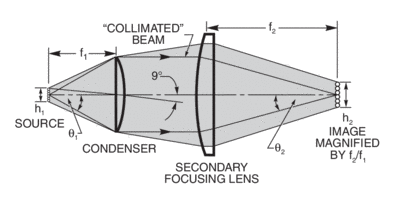
Fig. 1 shows a condenser collecting and collimating the light from one of our sources. In many applications, it is convenient to have a collimated path, which is used for placement of beam filtering or splitting components. Fig.15 shows a short collimated path, and a secondary focusing lens reimaging the source. As θh is invariant, the image size, h2, will be given by:
h2 = h1 θ1/ θ2
From the geometry:
h2 = h1 f2/ f1 (small angles assumed)
Monochromators and Filters with an Extended Source
Invariants are of particular value when designing systems in spectroscopy. Monochromators have acceptance angles, slit heights, and slit widths set to give desired resolution. These define the value of the optical extent G, of the monochromator, and allow comparison of different systems and selection of light source optics. The comparison is no longer simply based on F/# of the monochromator. A low F/# monochromator may have lower optical extent, i.e., less throughput, than a monochromator with higher F/#, but which uses larger slits to give the desired resolution. For example, our 1/8 m and our 1/4 m Monochromators have approximately the same F/# but the 1/4 m has a higher Glim for the same resolution.
The advantages of an optical filter are quickly apparent in the following example:
Example
Compare the 56430 Narrow Band Filter with the 77250 1/8 m Monochromator for isolation of a 20 nm bandwidth at 365 nm from an extended source. The monochromator has a standard 1200 l/mm grating.
The acceptance angle of this filter for the 20 nm bandwidth is approximately 15°. The corresponding solid angle is 0.21 sr. If the filter holder reduces the aperture to 0.9 inch (22.9 mm), the area is 4.1 cm2 and
Gfil = 0.86 sr cm2
We must multiply this by the filter transmittance of 0.2 for comparison of throughput.
Gfil Tfil = 0.17 sr cm2
The acceptance angle of the 77250 Monochromator is 7.7° and the corresponding solid angle is 0.57 sr. For a 20 nm bandwidth, the slit width is 3.16 mm. As the usable slit height is 12 mm, the area is 0.38 cm2, so:
Gmono = 0.022 sr cm2
and
Gmono Tmono = 0.007 sr cm2
The optical filter isolating 20 nm from this extended source passes about 24 times as much light as the monochromator. If the light from the filter can be coupled to a detector, i.e. the detector does not restrict the system, then the filter is much more efficient.
This ratio does not apply to small asymmetrical sources such as the arcs of our arc lamps. Each source must be examined individually.


